기초 지식 1. 이미지를 한 점으로 보기
제목부터가 무슨 말같지도 않은 소리인가 싶죠? 그런데 이 과정은 AI를 하는 데에 큰 직관을 던져 줍니다. 이미지를 한 점으로 보라는 말이 무슨 말일까요? 아래 2차원을 기준으로 생각 해볼게요.

2차원 상의 하나의 직선이 있습니다. 그림 1. 과 같죠. 이 직선을 a라 하겠습니다. 이 그림1의 직선을 하나의 축을 늘려 3차원에서 표시해 보겠습니다. 그럼 그림 2와 같은 형태가 될겁니다. 그림 2의 상황에서 직선 a의 법선 벡터 방향을 같는 평면을 하나 그려보죠. 해당 평면을 D라고 합시다. 그럼 3은 평면 D에서 본 직선의 모습을 나타냅니다. 즉 직선 a는 평면 D의 입장에서는 하나의 점이 되는 겁니다.
여기까지는 이해가 됐죠? 직선은 y = ax + b로 나타나며 이는 벡터로 표현하면 y = a x 로 표현이 가능하죠. 이 때 굵게 쓰여진 글씨는 벡터를 의미합니다. 좋아요 여기까지 따라오셨죠? 조금 어려워집니다.
이미지는 어떻게 표현될까요? 픽셀로 나타납니다. 아래와 마찬가지로 말이죠. 쉽게 생각하기 위해 이미지는 2( 높이 )x2( 넓이 )x3 ( 채널 ) 으로 나타날수 있다고 합시다.

그럼 위의 이미지를 표현하는 방법은 무엇일까요? tensor라는 개념이 도입됩니다. 우리는 이미지를 3차원 tensor로 나타낼 수 있죠. tensor는 데이터의 배열이라고 할 수 있습니다. 0차원은 scalar, 1차원은 벡터, 2차원은 matrix, 3차원부터는 3-tensor라고 하죠. 참고로 tensor에서 상위 차원은 하위차원을 요소로 가집니다. 즉 1차원 벡터에서는 요소로 scalar를 2차원 matrix에서는 1차원 벡터를 요소로 가지지요. 차원 수는 rank라고 합니다. 우리가 언급했던 직선은 tensor의 입장에서는 1차원입니다. 벡터로 직선을 표현할 수 있으니까요. 뭐 tensor는 이정도로만 정리하고, 다시 이미지로 돌아가 이미지는 3개의 차원을 가집니다. 즉 차원은 HxWxC 의 차원을 가지게 되죠. H는 높이, W는 넓이, C는 채널입니다. 여기서 채널은 R, G, B 가 되겠죠? 그러면 하나의 이미즈는 H x W x C 개 만큼의 숫자로 이루어진 하나의 tensor가 되겠죠. 그럼 이 tensor를 하나의 점으로 보고 싶으면 어떻게 하면될까요? 위에서 적용했던 아이디어와 같이 이미지의 숫자 개수보다 큰 차원에서 그 tensor를 바로보면 됩니다. 앞의 내용을 상기해 볼까요? 직선은 1 차원 tensor로 볼 수 있습니다. 다만 1차원 tensor에 2 개의 component가 존재할 뿐이죠. 그럼 2차원에서 1차원 tensor를 바라보게 되면 하나의 점으로 보이듯, 이미지를 그보다 한차원 위에서 보면 점으로 볼 수 있게 되는 거죠. 위 이미지는 4 차원 tensor의 입장에서 본다면 하나의 점으로 볼 수 있는겁니다. 그럼 여기까지는 알겠나요?? 그런데 궁금한 점이 있을겁니다.
왜? 점으로 봐야할까?
기초 지식 2. 이미지를 점으로 보는 것에 대한 관점
다시 한번 아래 그림을 볼까 요?
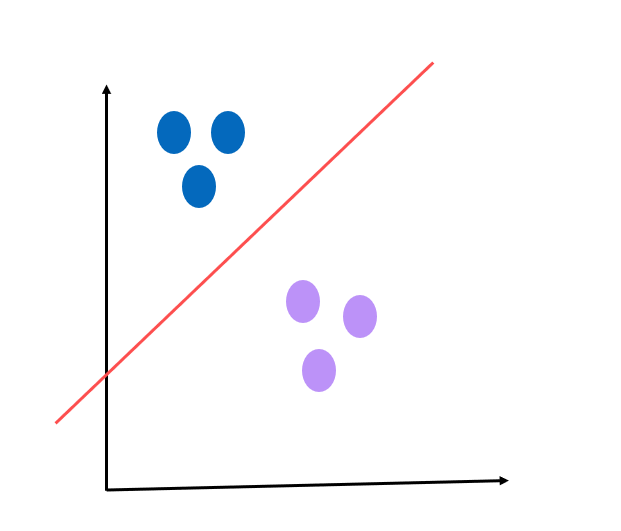
그림 4를 보면 6개의 점이 있고 가운데 하나의 선이 지나갑니다. 즉 점으로 나타내게 되면 위와 같이 선으로써 공간을 구분할 수 있게 되죠. 즉 선을 기준으로 왼쪽 위 공간은 파란색 점을 위한 공간, 오른쪽 아래는 보라색 점을 위한 공간으로 구분할 수 있다는 거죠. 그럼 이제 왜 이미지를 점으로 봐야하는가에 대한 목적을 이 직관으로부터 얻을 수 있게되죠. 우리가 하려고 하는 것은 4차원 공간에서 각 이미지를 점으로 놓고 그 공간을 구분할 선을 통해 공간에 따라 분류( classification )를 하려고 하는 것이죠.
이번 기초 이론을 통해 이미지를 왜 점으로 봐야하는 가에 대해 정리해봤습니다. 다음 이론에서는 어떻게 저 선을 만들 수 있는지에 대해 알아보도록 할게요! 그럼 다음글에서 뵈요!
참고 블로그

