논문 원문 : https://arxiv.org/abs/1708.02002
Loss function 에 대해
한글로 하면 손실함수가 되겠네요. 손실 함수는 무엇인가 와닿지 않아요. 도대체 loss function의 역할이 무엇일까요? loss function( 손실 함수 )은 우리가 만든 분류기 ( classifier )에 대한 평가 지표라고 생각하시면 됩니다. 분류기에 대한 내용은 후에 다루도록 할게요. 오늘 주는 그게 아니니까요. 즉 평가 지표는 평가 지푠데, 얼마나 구린가에 대한 평가 지표입니다. loss가 크다면, 분류기는 해당 식이 정의한 정의 내에서는 분류를 잘하지 못한다라고 생각할 수 있는거죠. 그런데 loss function은 좀더 수학적으로 설명하면 무엇일까요? 실제 값과 예측 값의 차이를 말합니다. 실제 분포와 예측 분포의 차이를 말하기도 하고요.
Base knowledge : Cross entropy loss
Focal loss는 논문에 의하면 CE loss에서 시작합니다. 그럼 CE loss는 무엇일까요? 이를 알기 위해 information과 Entropy에 대해 알아야합니다. information은 정보량을 말하는 데, 어떤 사건을 수치로 나타낸 것을 말합니다. 사건을 수치로 나타낸 다는 말은 확률을 이용해 나타낸다는 것이죠. 또한 정보량의 특징을 알아야 합니다. 정보량은 드물게 발생하는 사건일수록 새롭게 얻는 정보가 많다는 특징을 가지죠. 꽤나 직관적입니다. 매우 자주 발생하는 사건에 대해서는 알게 없다는 말과도 같으니까요. 이를 수식으로 표현해볼까요?
Information
특정 사건이 일어날 확률을 p(x) 라고 합시다. 그럼 정보량은 어떻게 표현하면 될까요? 사건이 일어날 확률이 높으면 정보는 적어지니까 간단하게 반비례한다고 생각하여, 1/p(x) 로 나타내면 되지 않을까요? 정보량은 1/p(x) 로 나타내면 편할 것 같아요. 그런데, 이번에는 두 가지 사건이 일어났다고 해보죠. 정보량을 확률로 나타내게 되면 두 사건이 일어났을 때 정보를 얻으려면 어떻게 해야할까요? 확률로 나타냈기 때문에 곱해야하죠. 그런데 이는 직관적이지 않죠. 사건이 일어났을 때 두 정보를 더해는 것이 직관적이잖아요? 그럼 기존 정보량에 log를 취해봅시다. 로그의 특징으로 인해 곱을 합으로 바꿀 수 있게 되었습니다. 보다 직관적이 되었달까요? 결국 information = log( 1/p(x) ) = - log ( p(x) ) 가 되겠습니다. 정보량은 확률 분포를 의미하기도 합니다. 왜냐하면 초콜렛 1, 사탕 99 일 때의 정보량, 초콜렛 50, 사탕 50 일 때의 정보량. 이렇게 각각의 개수에 따라 정보량이 달라지기 때문입니다.
Entropy
정의부터 말씀드리고 가자면 Entropy는 정보량의 기대값을 의미합니다. 식으로는 아래와 같죠?

X 가 -log ( p(x) ) 로 바뀌면 x 가 -log ( p (x) ) 로 바뀌죠. 뭐 그건 그렇다는 것이고 수식으로만 설명하면 이해가 안가니까 생각해봅시다. 정보 entropy는 정보량의 기대값, 즉 평균 정보량이죠. 그런데 물리에서 entropy란 용어는 불확실성을 표현할 때 쓴단 말이죠? 자 이제 왜 서로 동등한지 생각해봅시다. 정보의 불확실성이 크다라는 의미를 생각해보죠. 이는 즉 어떤 정보를 얻었을 때 그를 예측하기 쉽지 않다라는 말과 같습니다. 예를 들어보죠. 가방에 사탕과 초콜렛 모두 합쳐 100개가 들어 있습니다. 만약에 초콜렛과 사탕이 50 개씩 들어 있다면, 하나를 꺼냈을 때, 초콜렛일지, 사탕일지 예측하기 어려워지죠. 이는 정보 엔트로피가 높은 상황입니다. 그럼 이번에는, 초콜렛이 99개 사탕이 1개가 있다고 해보죠. 그럼 가방에서 무엇인가를 꺼낸다면 초콜렛일 확률이 높다는 것을 예측할 수 있겠죠. 이 상황은 정보 엔트로피가 낮은 상황입니다. entropy를 식으로 나타내면 아래와 같습니다.
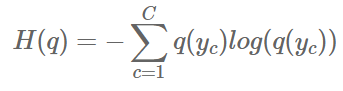
q( y_c ) 라는 사건이 일어날 확률에 정보량 ( 사건이 일어날 확률 분포 ) 를 곱해준 것이죠. 이는 수식적으로는 위에서 말한 특정 확률 변수의 기댓값을 구하는 것과 같습니다. 이번에는 기대값 입장에서 위의 상황을 다시 설명해 보죠. 다시 그 상황을 간략하게 설명하사면, 초콜렛은 99개 사탕은 1개가 있는 상황입니다. 정보량은 발생할 확률이 높을수록 적습니다. 그럼 초콜렛은 정보량이적고, 사탕은 정보량이 높겠죠. 그런데 앞에 곱해지는 사건의 확률은 초콜렛은 높고 사탕은 낮죠. 그럼 이들을 곱해주게 되면 정보 기대값은 낮아지게 되는 거죠. 반대로, 정보가 골고루 퍼져있을 수록 정보량도 커지고 확률은 낮아지게 되죠. 그렇다면 기대값의 입장에서는 큰 값과 작은 값이 곱해짐으로 값이 작아지게 됩니다. 반대로 50개씩 가지고 있는 경우 정보량은 서로 비슷해지고 확률 역시 비슷해 짐으로써 둘이 곱했을 때 역시 비슷한 것끼리 곱했기에 커진다고 생각해 주시면됩니다. 쉽게 그냥 정규확률 분포에서 가장 높은 점이 가운데라는 점을 떠올려 주시면 되겠네요. 여기서 알수 있는 직관은 가장 고른 분포에서 정보의 기대값이 가장 높으며, 이는 다음 정보에 대한 불확실성이 가장 높은 상황이라고 여길 수 있는 겁니다. 물론 곱해지는 값의 영향력에 따라 낮은 값과 높은 값이 곱해지더라도 높은 값을 가질 수 있지만, 이는 log와 확률의 값의 범위를 생각해 보시면 누가 더 큰 영향력을 끼치는가에 대한 직관을 얻게 될 겁니다.
Cross Entropy

시작하기에 앞서 cross Entropy는 예측과 실제가 다르기에 얻어지는 정보량의 기대값을 말합니다. 이제 위의 내용들을 다가지고 와서 생각해봅시다. p 사건에 대한 정보량이 있는 상황에서 사건 q가 발생할 확률에 대해서 생각해봅시다. 즉 정보량 p가 주어진 상황에서의 q에 대한 기대 값을 구하는 상황을 말씀드리는 것이고, 이가 바로 cross entropy이죠. 이게 무슨 개소리냐, 그러니까 원래는 사건 q에 대해 확률 분포가 정해져 있죠. 즉 사건 q에 대해서는 정보량 q를 가지고 그 기대값을 구하는 게 맞다는 소립니다. 마찬가지로 p 역시 사건이 일어날 확률과 정보량 p에 대해 정해져 있기때문에 정보의 기대값은 정해져 있는 것이죠. 예시로, 특정 사건 p에 대한 정보량이 적다면 특정 사건 p는 일어날 확률이 크겠죠? 위에서 한 내용이에요. 그런데 cross entropy에서 하고자하는 일은, 예측 값 q를 가지고 p에 대한 정보량을 알고자 하는 것이란 말이죠. 그럼 왜 차이를 의미하는 가는 쉽습니다. 자 하나만 짚고 넘어갑시다. q가 일어날 확률이 크다면, q의 정보량은 적고 기대값은 낮다는 겁니다. 그럼 정보량 p가 q와 일치하지 않는다면 정보의 기대값은 커지는 효과가 발생하게 됩니다. 이해를 돕기 위해 왜 그런가에 대해 숫자로 설명해보면, 확률 분포( 정보량 )에서 가질수 있는 가장 큰 값은 무한대이고, 확률은 가질 수 있는 가장 큰 값은 1 이죠. p(y_c) = 1 이라고 한다면, 1-p(y_c) = 0 이 되겠죠? 그럼 log를 취하면 전자는 1 후자는 infinte value 가 될 거에요. 만약 q 분포가 p 분포와 일치한다면, 위에 entropy에서 언급한대로 작은 값이 나오게 되겠죠. 그렇지만, 다르게 된다면, 큰 값이 나오게 될거에요. 왜냐하면, 다르다는 거는 q와 p의 차이가 크다는 소리인데, q가 크면 p가 작고 p가 작으면 log( p ) 가 커질 것이고 그렇게 되면 q * log( p ) 가 커지고 , p가 크고 q 가 작다면 (1- q ) log(1-p(y_c)) 가 커질테니까요. 즉 p 와 q 의 차이가 클수록 큰 값이 나오게 되는 결과가 나오는 것이죠. 그럼 왜 cross entropy가 loss function으로 사용되는지 이해하셨을까요? 이제 한발 시작했어요. 다음 글에서는 조금 더 나아가서 한번 파헤쳐보도록 하자구요.
'visioin_ai이론' 카테고리의 다른 글
| [ ai 기초 ] AI의 정체는? ( feat. 수학이 필요한 이유, 확률과 통계, 선형 대수 ) (0) | 2023.10.26 |
|---|---|
| [ computer vision AI ] focal loss 파헤치기 2 ( feat. Balanced Cross Entropy , focal loss ) (0) | 2023.01.04 |
| computer vision ai 기초 이론 1. 이미지를 점으로 보기 (0) | 2023.01.02 |

